大家知道福尔摩斯吗？

他有一句名言是：“When you have eliminated the impossibles,whatever remains,however improbable,must be the truth.”（当你排除一切不可能的情况，剩下的不管多难以置信，那都是真相。）

这也暗示了他在探案过程中的惯用手法：在归纳出几个可能的假设之后，一个接一个地进行排除。

近年来，人工智能专家在从证据到假设、从结果到原因的自动化推理方面取得了相当大的进展，而实现该功能所必需的一项基本工具，就是上期分享中我们所初识的——贝叶斯网络。

本篇分享将结合应用实例，讲述贝叶斯网络从18世纪其发展根源，到20世纪80年代其蓬勃发展的故事。

2014年7月17日，马来西亚航司的一架航班在乌克兰东部上空坠毁，机上所有人员遇难。

尸体被严重烧毁，DNA信息遭到破坏；加之现场是战区，法医专家只能不定时地进入坠机地点附近的有限范围内搜查，调查人员困难重重。

幸运的是，法医研究所的科学家有一个强大的工具——波拿巴，它是目前最先进的遇难者身份识别程序。该软件利用贝叶斯网络进行自动化推理，能够综合比对来自遇难者几个不同的家庭成员的DNA信息。

归功于波拿巴的精确和高效，法医研究所能最终在2014年12月识别出298名遇难者中294人的身份。

贝叶斯网络，其影响着我们生活的许多方面。它广泛应用于语音识别软件、垃圾邮件过滤器、天气预报、潜在油井位置评估以及美国食品和药物管理局对医疗器械的审批过程。

贝叶斯网络与因果图之间的关系很简单。因果图就是一个贝叶斯网络，其中每个箭头都表示一个直接的因果关系，或者至少表明了存在某个因果关系的可能性。但反过来，并非所有的贝叶斯网络都是因果关系网络。

贝叶斯统计的创立者，托马斯·贝叶斯，是一位长老会牧师。他对统计推理的主要贡献是使用了"逆概率"（inverse probability）这个概念，并把它作为一种普遍的推理方法提出来。

1793年，《哲学汇刊》刊载了他有关逆概率的遗作。在这篇文章发表前，苏格兰哲学家大卫·休谟在1748年写了一篇题为《论神迹》的文章，其中指出“本质上不可靠的证据是不能推翻衍生于自然法则，诸如'人死不能复生'这样的命题的。”

对于贝叶斯来说，休谟的观点很自然地引发了一个福尔摩斯式的问题：

需要多少证据才能让我们相信，我们原本认为不可能发生的事情真的发生了？

在何种情况下，某个假设才会越过绝不可能的界限抵达不大可能，甚至变为可能或确凿无疑呢？

贝叶斯的论文表明了，我们可以从一个果推断某个因的概率。如果我们知道因，那我们很容易就能估计出果的概率，这是一个前向概率（forward probability）。而它的反面，也就是贝叶斯时代的“逆概率”推理，则难度要大得多。

他以台球为例，向我们证明了逆概率推理是可行的，并展示了如何操作。

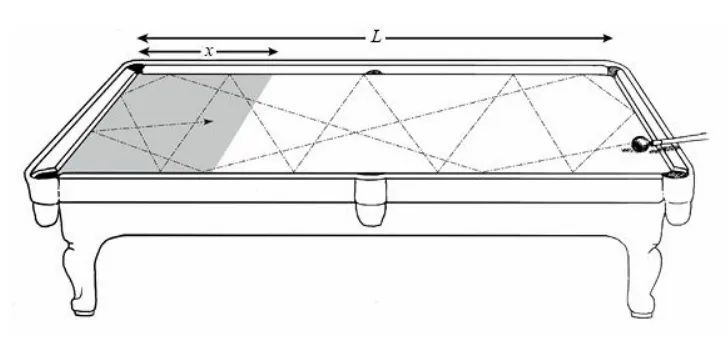
打台球的时候，假设台球会在桌面上经多次反弹曲折行进，我们无法确定它最终会停在哪里。那么，球在距桌子左端x英尺这个范围内停下来的概率是多少？

如果我们知道桌子的长度，且桌子十分平滑，那么这就是一个非常简单的问题（见下图）。对物理学的直观理解告诉我们，一般来说，如果桌子的长度为L英尺，球在距桌边缘x英尺范围内停止的概率是x/L。

例如，在一个长12英尺的台球桌上，球在距桌边缘1英尺范围内停下来的概率1/12；在一个长8英尺的台球桌上，这个概率就是1/8。

一方面，桌子的长度越长，这个概率就越低，因为球可以停止的位置越来越多。另一方面，x越大，这个概率就越高，因为球的可停止区域越来越大。

如果从逆概率问题角度考虑，问题则变成了：我们观察到球的最后停止位置在距桌边缘x=1英尺的范围内，但桌子的长度L未知。此时，桌子长度为100英尺的概率是多少？

常识告诉我们，L更可能是50英尺，而不是100英尺，但具体的可能性无从知晓。

为什么前向概率（已知L求x的概率）比逆概率（已知x求L的概率）更容易估算？在这个例子中，这种不对称性来自L为因x为果这一事实。

例如，若我们观察到一个因（男孩向窗户扔球），大多数人可以预测到果（球可能会打破窗户），人类的认知就是在这个方向上运作的。

但若给定了果（窗户破了），要求我们推断因，就需要更多的信息才能进行推断（窗户是被球打破的吗？是谁扔球打破了窗户？），解决这个问题需要我们拥有福尔摩斯的头脑去追踪所有可能的因。

贝叶斯致力于打破这种认知不对称，并提出了一种即使并非数学天才也能使用的估算逆概率方法。

在下期分享中，我们将从更多实例出发，深入了解贝叶斯网络。